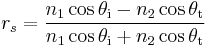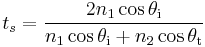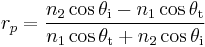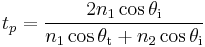Fresnel equations

The Fresnel equations (or Fresnel conditions), deduced by Augustin-Jean Fresnel ( /frɛˈnɛl/), describe the behaviour of light when moving between media of differing refractive indices. The reflection of light that the equations predict is known as Fresnel reflection.

1 Overview
2 Definitions and power equations
- 2.1 Special angles
3 Amplitude equations
- 3.1 Conventions used here
- 3.2 Formulas
4 Multiple surfaces
5 See also
6 References
7 External links

Overview

When light moves from a medium of a given refractive index n₁ into a second medium with refractive index n₂, both reflection and refraction of the light may occur. The Fresnel equations describe what fraction of the light is reflected and what fraction is refracted (i.e., transmitted). They also describe the phase shift of the reflected light.

The equations assume the interface is flat, planar, and homogeneous, and that the light is a plane wave.

Definitions and power equations

In the diagram on the right, an incident light ray PO strikes at point O the interface between two media of refractive indices n₁ and n₂. Part of the ray is reflected as ray OQ and part refracted as ray OS. The angles that the incident, reflected and refracted rays make to the normal of the interface are given as θ_i, θ_r and θ_t, respectively. The relationship between these angles is given by the law of reflection: θ_i = θ_r; and Snell's law: sin(θ_i)/sin(θ_t) = n₂/n₁.

The fraction of the incident power that is reflected from the interface is given by the reflectance R and the fraction that is refracted is given by the transmittance T.^[1] The media are assumed to be non-magnetic.

The calculations of R and T depend on polarisation of the incident ray. If the light is polarised with the electric field of the light perpendicular to the plane of the diagram above (s-polarised), the reflection coefficient is given by

$R_\mathrm{s} = \left(\frac{n_1\cos\theta_{\mathrm{i}}-n_2\cos\theta_{\mathrm{t}}}{n_1\cos\theta_{\mathrm{i}}%2Bn_2\cos\theta_{\mathrm{t}}}\right)^2 =\left[\frac{n_1\cos\theta_{\mathrm{i}}-n_2\sqrt{1-\left(\frac{n_1}{n_2} \sin\theta_{\mathrm{i}}\right)^2}}{n_1\cos\theta_{\mathrm{i}}%2Bn_2\sqrt{1-\left(\frac{n_1}{n_2} \sin\theta_{\mathrm{i}}\right)^2}}\right]^2$ ,

where the second form is derived from the first by eliminating θ_t using Snell's law and trigonometric identities.

If the incident light is polarised in the plane of the diagram (p-polarised), the R is given by

$R_\mathrm{p} = \left(\frac{n_1\cos\theta_{\mathrm{t}}-n_2\cos\theta_{\mathrm{i}}}{n_1\cos\theta_{\mathrm{t}}%2Bn_2\cos\theta_{\mathrm{i}}}\right)^2 =\left[\frac{n_1\sqrt{1-\left(\frac{n_1}{n_2} \sin\theta_{\mathrm{i}}\right)^2}-n_2\cos\theta_{\mathrm{i}}}{n_1\sqrt{1-\left(\frac{n_1}{n_2} \sin\theta_{\mathrm{i}}\right)^2}%2Bn_2\cos\theta_{\mathrm{i}}}\right]^2$ .

As a consequence of the conservation of energy, the transmission coefficient in each case is given by T_s = 1 − R_s and T_p = 1 − R_p.^[2]

If the incident light is unpolarised (containing an equal mix of s- and p-polarisations), the reflection coefficient is R = (R_s + R_p)/2.

For common glass, the reflection coefficient is about 4%. Note that reflection by a window is from the front side as well as the back side, and that some of the light bounces back and forth a number of times between the two sides. The combined reflection coefficient for this case is 2R/(1 + R), when interference can be neglected (see below).

The discussion given here assumes that the permeability μ is equal to the vacuum permeability μ₀ in both media. This is approximately true for most dielectric materials, but not for some other types of material. The completely general Fresnel equations are more complicated.

Special angles

Main articles: Brewster's angle and Total internal reflection

At one particular angle for a given n₁ and n₂, the value of R_p goes to zero and a p-polarised incident ray is purely refracted. This angle is known as Brewster's angle, and is around 56° for a glass medium in air or vacuum. Note that this statement is only true when the refractive indices of both materials are real numbers, as is the case for materials like air and glass. For materials that absorb light, like metals and semiconductors, n is complex, and R_p does not generally go to zero.

When moving from a denser medium into a less dense one (i.e., n₁ > n₂), above an incidence angle known as the critical angle, all light is reflected and R_s = R_p = 1. This phenomenon is known as total internal reflection. The critical angle is approximately 41° for glass in air.

Amplitude equations

Equations for coefficients corresponding to ratios of the electric field amplitudes of the waves are also called "Fresnel equations". These take several different forms, depending on the choice of formalism and sign convention used. The amplitude coefficients are usually represented by lower case r and t.

Conventions used here

In this treatment, the coefficient r is the ratio of the reflected wave's complex electric field amplitude to that of the incident wave. The coefficient t is the ratio of the transmitted wave's electric field amplitude to that of the incident wave. The light is split into s and p polarizations as defined above. (In the figures to the right, s polarization is denoted " $\bot$ " and p is denoted " $\parallel$ ".)

For s-polarization, a positive r or t means that the electric fields of the incoming and reflected or transmitted wave are parallel, while negative means anti-parallel. For p-polarization, a positive r or t means that the magnetic fields of the waves are parallel, while negative means anti-parallel.^[3]

Formulas

Using the conventions above,^[3]

$r_s = \frac{n_1 \cos \theta_\text{i} - n_2 \cos \theta_\text{t}}{n_1 \cos \theta_\text{i} %2B n_2 \cos \theta_\text{t}}$

$t_s = \frac{2 n_1 \cos \theta_\text{i}}{n_1 \cos \theta_\text{i} %2B n_2 \cos \theta_\text{t}}$

$r_p = \frac{n_2 \cos \theta_\text{i} - n_1 \cos \theta_\text{t}}{n_1 \cos \theta_\text{t} %2B n_2 \cos \theta_\text{i}}$

$t_p = \frac{2 n_1\cos \theta_\text{i}}{n_1 \cos \theta_\text{t} %2B n_2 \cos \theta_\text{i}}$

Because the reflected and incident waves propagate in the same medium and make the same angle with the normal to the surface, the amplitude reflection coefficient is related to the reflectance R by

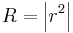$R=\left| r^2 \right|$ .

The transmittance T is generally not equal to 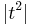$|t^2|$ , since the light travels with different direction and speed in the two media. The transmittance is related to t by

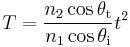$T=\frac{n_2 \cos \theta_\text{t}}{n_1 \cos \theta_\text{i}} t^2$ .

This equation reflects the fact that a pencil of rays changes diameter when it passes from one medium to another (except at normal incidence). In terms of the ratio of refractive indices, 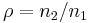$\rho = n_2/n_1$ , and the magnification of beam diameter at the interface, m,

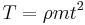$T = \rho m t^2$ .

Multiple surfaces

When light makes multiple reflections between two or more parallel surfaces, the multiple beams of light generally interfere with one another, resulting in net transmission and reflection amplitudes that depend on the light's wavelength. The interference, however, is seen only when the surfaces are at distances comparable to or smaller than the light's coherence length, which for ordinary white light is few micrometers; it can be much larger for light from a laser.

An example of interference between reflections is the iridescent colours seen in a soap bubble or in thin oil films on water. Applications include Fabry–Pérot interferometers, antireflection coatings, and optical filters. A quantitative analysis of these effects is based on the Fresnel equations, but with additional calculations to account for interference.

The transfer-matrix method, or the recursive Rouard method^[4] can be used to solve multiple-surface problems.

References

^ Hecht (1987), p. 100.
^ Hecht (1987), p. 102.
^ ^a ^b Lecture notes by Bo Sernelius, main site, see especially Lecture 12.
^ see, e.g. O.S. Heavens, Optical Properties of Thin Films, Academic Press, 1955, chapt. 4.

Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. ISBN 0-201-11609-X.
Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. ISBN 0-321-18878-0.

External links

Fresnel Equations – Wolfram
FreeSnell – Free software computes the optical properties of multilayer materials
Thinfilm – Web interface for calculating optical properties of thin films and multilayer materials. (Reflection & transmission coefficients, ellipsometric parameters Psi & Delta)
Simple web interface for calculating single-interface reflection and refraction angles and strengths.
Reflection and transmittance for two dielectrics – Mathematica interactive webpage that shows the relations between index of refraction and reflection.